Sudoku Players' Forum (clone)

.
Forcing T&E

In my books "Constraint Resolution Theories" ([CRT]) and "Pattern-Based Constraint Satisfaction and Logic Puzzles" ([PBCS], both versions), I introduced two patterns I called forcing-whips, resp. forcing-braids, made up of a (3D-)bivalue cell and two whips (resp. two braids) with respective targets the two candidates of the bivalue cell.
I noticed that the associated resolution rules (eliminating common left-linking candidates and asserting common right-linking candidates) were of little use in practice, because in all the cases I tried, a solution with shorter whips/braids was available. I have no new data to change my conclusions about this result.

Three things I didn't consider at the time of the above publications were:
- a definition of Forcing-T&E(cand1, cand2): start from a bivalue pair of candidates (cand1, cand2), develop independently the T&E branches starting from each candidate, eliminate all the candidates eliminated in both branches, assert all the candidates asserted in both branches.
- a proof that any elimination/assertion done by Forcing-T&E(cand1, cand2) can be done by some Forcing-braid(cand1, cand2) - the converse being obvious as usual.
- an extension of these definition and result to any theory T with the confluence property.
I will not insist on this, because all three points are obvious consequences or extensions of my various definitions and T&E vs braids theorems.

Forcing-whips/braids are not very interesting as long as they respect the natural notion of length and as long as one uses the simplest-first strategy that rely on it.

However, there has been recently some interest for various forcing-things of uncontrolled length - under the name of conjugated tracks or no name at all. I've therefore coded Forcing-T&E in SudoRules. Contrary to Forcing-whips or Forcing-braids, I put no restriction on their length and they don't require that whips or braids be activated. You can see an example of application in the 4th post for the puzzle here: http://forum.enjoysudoku.com/4-leaf-clover-8-4-t38586.html, where a single application of Forcing-T&E(Subsets) is enough to solve the puzzle.

Needless to say, this is not my preferred resolution technique.

a reader of PBCS and an apparently silent follower of this forum (summarised) wrote:What's the difference/relationship between your Forcing-T&E, your Forcing-braids and the forcing-chains of Sudoku Explainer?
(Subsidiarily, how do "tracks" fit in the landscape?)

First, note that anything I will say about Sudoku Explainer (SE) is relative to my interpretation of how it works (and it is NOT intended as a criticism of it as a common reference for everyone here; considering the time when it was developed, it remains a remarkable point in the history of Sudoku and it is still a very useful tool).
I have once had a look at the Java code and I couldn't see any line of documentation. As I didn't feel like reverse-engineering it, and as there is AFAIK no available documentation about what the implemented rules do, what I'll say is based upon the output you can see when you try to solve a puzzle.
What SE does is apply successively some "rules" in an order defined by some ranking of the rules. As far as I can understand, this ranking is based on:
- for classical rules (Singles, Subsets [including Fish], XY-wing, XYZ-Wing, Uniqueness, ...): some arbitrary convention
- for the (various types of) chain rules (be they named as forcing or not): the number of inferences necessary for reaching a conclusion; as this would be too fine grained, these numbers are cluttered into groups, all the elements of which are given the same SE rating. As far as I can tell, the groups of same rating are totally arbitrary (and I've noticed in PBCS some queer effects of this arbitrariness).

Any precision or correction of the above is welcome.


Now, let me answer the question. The first step is to realise that "Forcing" doesn't play any role in the comparison. The comparison with "Forcing" is a straightforward consequence of the comparison of the chains/techniques without "forcing" in their names.

I would say that T&E and braids (which have the same resolution power) are the two extremes on a scale of controlling the length of techniques/patterns: totally uncontrolled in the T&E procedure vs totally controlled in the braid pattern.

Regarding SE, there is some control in the size of the various "contradiction chains" it uses, but the essential difference between "contradiction chains" and braids is about the nature of this control: in a braid, it is the number of CSP-Variables it uses (it can be defined in pure logical terms and this is used to define the length of the braid); in SE, it is the number of inference steps used by the "contradiction chain" (which can in no way be defined in logical terms).

(Remember that, in Sudoku, a CSP-Variable is represented by a 2D-cell in my 324-cell Extended Sudoku Board).

The maximum length of braids necessary to solve a puzzle (the B-rating of the puzzle) is stable under isomorphisms (precisely because it can be defined in a purely logical way). It is well known that the SER is not.
While braids rely on a vison of chains as static patterns visible on the grid (possibly with some effort for the long ones), SE relies on an antiquated vision of chains as chains of inferences.
By moving away from that vision, braids (and most of my other chains) require some abstraction: once the z- and t- candidates have been used to allow the extension of a partial-braid, they are no longer useful for further extensions. Thats' why they can be forgotten in the representation of braids/whips.. and why all these chains can be represented as bivalue-chains (with the name of the pattern at the head of this representation, to recall what kind of chain they really are and how to read and check them on the current PM).


About the subsidiary question: if tracks and anti-tracks are defined as sets, as Robert persists to do, they are no more than anti-T&E and T&E, respectively; and conjugated tracks are no more than Forcing-T&E.
However, the way Robert uses (anti-)tracks in practice is always as ordered sets, not developed to the full extent of a T&E procedure; which makes them move slightly towards the controlled side of the scale of control. However, I'm not aware of any publication of Robert about controlling the size of his tracks, so I wouldn't venture too much on this ground. He is welcome to state his view about it.

Hi Denis,

denis_berthier wrote:About the subsidiary question: if tracks and anti-tracks are defined as sets, as Robert persists to do, they are no more than anti-T&E and T&E, respectively; and conjugated tracks are no more than Forcing-T&E.
However, the way Robert uses (anti-)tracks in practice is always as ordered sets, not developed to the full extent of a T&E procedure; which makes them move slightly towards the controlled side of the scale of control. However, I'm not aware of any publication of Robert about controlling the size of his tracks, so I wouldn't venture too much on this ground. He is welcome to state his view about it.

I will try to answer you as precisely as possible for me.
Before I came to participate in this forum, I was content to discuss only one "component" of the Technique of Tracks (TDP), that of conjugated tracks which, in their most general approach, are two tracks P(E1) and P(E2) respectively issued from two distinct sets of E1 and E2 candidates such that the anti-track P'(E1UE2) is invalid. This is what you call, if I understand correctly, forcing-T&E and others forcing-net I think.
The reason is that, being exclusively interested in manual resolution, and therefore in a clientele of sudokists who practice this way, I didn't make the effort to go further in the reflection, except to introduce the bifurcations (or) when it gets complicated.
Such sets E1 and E2 include all those that form a partition of an entity (variable CSP rc), which gives wide possibilities of solving the puzzles usually tackled by manual solvers.
On the forum, I understood very quickly (more exactly I was made to understand) that T&E-forcing was frowned upon, the use of the contradiction (invalid track) too. So I exposed an aspect of TDP that I didn't really exploit, the use of the anti-track as the exclusive mode of resolution, this by stating the following rather obvious theorem :
If a candidate Z sees both a set of candidates E and a candidate B of the anti-track P'(E), Z can be eliminated.
In fact, this amounts to using two conjugated tracks of which only one P(E2)=P'(E1) is developed when E2 and E1 form a partition of an entity (variable CSP rc). So from this point of view the form has changed but not the content.
By seriously immersing myself in your work, which I hadn't really done before, I understood (not everything yet) the "simplest first" principle that underlies your whole theory and its fixed-length patterns.
I could with antitracks (and tracks as well as DEFISE does) design a fixed length antitrack pattern and use this "simplest first" principle, except that manually this is very tedious or impossible and intellectually it would be like plagiarizing your concepts.
For a manual resolution, the starting point are the "pairs" (partition E1, E2 of an entity, for example 2 candidates of the same cell) and as soon as we see that the anti-track coming from one of the two sets Ei develops, it would be absurd to abandon it under the pretext that we want to limit the number of candidates to n fixed in advance to come back to it later, so we exploit it to the detriment of its length. I understand that this can be called T&E, but it is already targeted T&E.
But another aspect is important to me, and that is the choice of target. Again, it is not a question of manually trying all the candidates to find out which ones can be targets.
Since the number of pairs is smaller, it is easier from a pair to find a target by constructing E and the antitrace P'(E) that will eliminate a target that is necessarily a candidate (or set of candidates) that sees both E and a candidate of P'(E).
This is the way I proceed in all the examples I have dealt with in this forum. I understand that this is called T&E because it is impossible to find E without trying, at least without analyzing the puzzle to mentally see that the choice of E is the right one. It is then a thoughtful T&E, a bit like in chess game one conceives a movement of the pieces after having analyzed the possibilities mentally. This naturally limits (memory limit) the number of candidates of the anti-track when solving the puzzle manually.
To conclude, if anti-trace is not a model of the types whip, g-whip, Sp-whip or braid, g-braid, Sp-braid, the way we can use it is close to, let's say, a pseudo-model, which makes me think about a resolution strategy based on this unique pseudo-model.
Cordialy
Robert

Mauriès Robert wrote: I understood (not everything yet) the "simplest first" principle that underlies your whole theory and its fixed-length patterns.

Indeed, the "(not everything yet) " is appropriate here because it's the exact opposite.

For any n ≥ 1, a predicate "whip[n]" can be defined by a first order formula in the language of Sudoku, but "whip" cannot (it would have to be an infinite disjunction of predicates whip[n]). Thus, the notion of length is inherent in the definition of a whip.
The same applies to any type of chain.
Whips (and other chain patterns) of fixed length have intrinsic, purely logic definitions, totally independent of the way they are used. Thats's why some theory can be developed about them.
And I've shown many examples where I use them with no predefined strategy. Similarly, I've said uncountably many times that a manual solver can use them as they come to him, if he doesn't care about finding the shortest chains.

The simplest-first strategy is a second layer of my approach. Combined with the confluence property, it allows to find the simplest (in the usual sense of "simplest hardest step" solution by following a single resolution path.
What's true is, SudoRules systematically uses this strategy, producing a rating at the same time as a solution - unless directed to do otherwise.

Mauriès Robert wrote:But another aspect is important to me, and that is the choice of target. Again, it is not a question of manually trying all the candidates to find out which ones can be targets.
Since the number of pairs is smaller, ...

Pairs of what? smaller than what?
If you were speaking of bivalue pairs of candidates, I would agree; there are fewer than the number of candidates.
But:

- bivalue pairs of candidates is not what tracks are about: you consider any partition E/E' of any cell. As you said: "Such sets E1 and E2 include all those that form a partition of an entity (variable CSP rc)" [it should be not only rc, but also rn, cn and bn). That makes a much higher number than the number of candidates, by one or two orders of magnitude; (unfortunately, most of them are useless). Admittedly, that makes them more general than my present definition of Forcing-T&E (it currently considers only pairs of candidates);

- the number of candidates (i.e. of potential targets) is not what counts for whips/braids... What counts is the number of partial-whips[1], a pattern very easy to identify on a grid (as easy as intersections) and with a number of instances much smaller than your above number of partitions of any cell and also much smaller than the number of candidates.

Mauriès Robert wrote:it is easier from a pair to find a target by constructing E and the antitrace P'(E) that will eliminate a target that is necessarily a candidate (or set of candidates) that sees both E and a candidate of P'(E).
This is the way I proceed in all the examples I have dealt with in this forum.

Actually, I have very strong doubts about this. If this was really the way you proceed, you wouldn't systematically find solutions with few steps.
What you really do is similar to what Defise does in his post-solution optimisation of whip solutions (a smart idea, but impractical for manual solvers).
You develop several resolution paths and you publish only the shortest one.

Mauriès Robert wrote: I understand that this is called T&E because it is impossible to find E without trying, at least without analyzing the puzzle to mentally see that the choice of E is the right one. It is then a thoughtful T&E, a bit like in chess game one conceives a movement of the pieces after having analyzed the possibilities mentally.

This comparison is totally misleading. No thoughtful analysis can allow you to develop mentally several Forcing-T&E solutions. Unless you're an alien from some as yet undiscovered galaxy, with brains extending through the whole body, under cover on Earth as a Sudoku solver, the best you can mentally foresee is the various results of single pairs; you can't mentally foresee several steps in advance.

Mauriès Robert wrote: [...] which makes me think about a resolution strategy based on this unique pseudo-model.

Looking forward to hearing of such a human-applicable strategy.

Hi Denis,
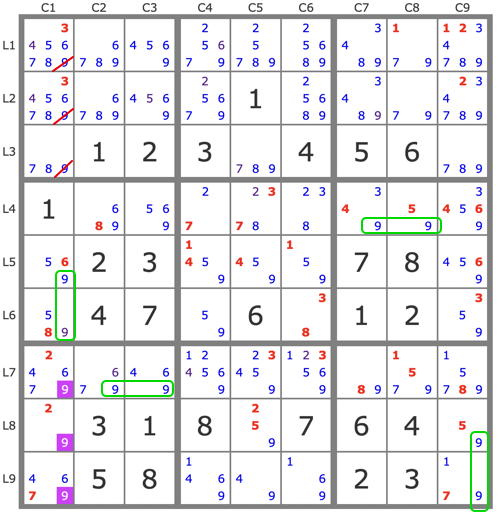
Indeed, I wasn't specific enough when I wrote that the number of pairs was lower. Indeed, it is not a question of examining all the possible partitions of the entities, but those that are likely to generate tracks or anti-tracks, what I would call "exploitable pairs". These pairs are less numerous than the puzzle candidates, which are all likely to be targets. These pairs are mainly the pairs of candidates, the pairs of set of candidates aligned in the same block, but not only as in this example on the puzzle on page 229 of PBCS :


On this puzzle, we see several pairs of sets of aligned candidates, such as for example E1=9c1b7 and E2=9r7b7 for which the antitrack P'(E1) allows the elimination of 9c1b1, which is done "visu".
So when I write "This is the way I proceed in all the examples I have treated in this forum", I wanted to say that by proceeding as I have just done on this example, I find the target among all the candidates likely to be eliminated by the choice of the set generating the anti-track. But I am not saying that the resolution I am presenting is the one that I found first, it is an evidence that I have optimized it because it is the only one that is of interest.
Robert
[Edit] Text corrected due to the error reported by DEFISE

Mauriès Robert wrote:Indeed, I wasn't specific enough when I wrote that the number of pairs was lower. Indeed, it is not a question of examining all the possible partitions of the entities, but those that are likely to generate tracks or anti-tracks, what I would call "exploitable pairs". [...]These pairs are less numerous than the puzzle candidates, which are all likely to be targets.

Once again, candidates are not the starting point for finding whips/braids. The starting point is a partial-whip[1] or a partial g-whip[1] and both are mere bivalue-cells (in rc, rn, cn or bn space) or alignments (i.e. g-bivalue-cells).
As a result, the number of starting "points" for whips.. is less than what you describe here, as you add all possible Subsets in the landscape of "exploitable pairs".
Needless to say that in addition to this additional complication at the very start, for each pair of conjugated tracks, you have to develop two T&E procedures in parallel and to keep comparing their results. I can't see any real advantage for a human solver.

Mauriès Robert wrote:I am not saying that the resolution I am presenting is the one that I found first, it is an evidence that I have optimized it because it is the only one that is of interest.

At least, we agree on something.

denis_berthier wrote:Once again, candidates are not the starting point for finding whips/braids. The starting point is a partial-whip[1] or a partial g-whip[1] and both are mere bivalue-cells (in rc, rn, cn or bn space) or alignments (i.e. g-bivalue-cells).
As a result, the number of starting "points" for whips.. is less than what you describe here, as you add all possible Subsets in the landscape of "exploitable pairs".

Of course, first of all I am interested in bivalve cells, then if necessary in alignments (g-bivalve cells) and if necessary in other partitions.

denis_berthier wrote:Needless to say that in addition to this additional complication at the very start, for each pair of conjugated tracks, you have to develop two T&E procedures in parallel and to keep comparing their results. I can't see any real advantage for a human solver.

No, resolutions based on the exploitation of an anti-runway require the development of only one procedure, that of the anti-runway. If I decide to develop two conjugated tracks, the advantage is usually a greater number of simultaneous eliminations, or even simultaneous validations. See for example http://forum.enjoysudoku.com/diagonals-centres-t38366.html page1.

Having said that, show me on a concrete example how you solve a puzzle "by hand" without Sudorules, certainly I would understand better how you find the targets.
Cordialy
Robert

Mauriès Robert wrote:Having said that, show me on a concrete example how you solve a puzzle "by hand" without Sudorules, certainly I would understand better how you find the targets.

Once again, you fail to understand the main point. It's not about finding the targets; it's about starting a chain pattern. The potential targets are a consequence of this starting partial-whip[1] or partial--whip[1] pattern - a pattern as easy to find as alignments or bivalue cells.
And there's no difference with how you find them, be they mere tracks, anti-tracks, or conjugated tracks.

It seems what you fail to understand is that my formal definitions start from the target, but that doesn't imply the patterns have to be found by first choosing a target.

Hi Denis,

denis_berthier wrote:Once again, you fail to understand the main point. It's not about finding the targets; it's about starting a chain pattern. The potential targets are a consequence of this starting partial-whip[1] or partial--whip[1] pattern - a pattern as easy to find as alignments or bivalue cells.
And there's no difference with how you find them, be they mere tracks, anti-tracks, or conjugated tracks.

It seems what you fail to understand is that my formal definitions start from the target, but that doesn't imply the patterns have to be found by first choosing a target.

I understand very well that a schema is a sequence of CSP variables V1, V2,... Vn such that Vn is empty if Z is solution, so that since we can identify an alignment and the targets it eliminates, we can identify longer sequences that will lead to eliminations. Nevertheless, the sequence must meet certain conditions to constitute a model. Among these conditions is the fact that in the left-hand candidates of Vi the z-candidates are not taken into account if they exist, so it is good that at this stage we already know which target is to be eliminated. One cannot therefore design a whip without knowing which target it eliminates as one designs an x-wing independently of the candidates it eliminates.
An example to illustrate what I say with the whip [3] of your resolution in paragraph 8.8.3.2 of your book.
The sequence of this whip [3] is V1=r6c4, V2=r5c5, V3=r9c5. To ensure continuity between V1 and V2 you must ignore the 9 of r5c5 so you take into account 9r4c5 to say that this sequence constitutes a whip [3] which eliminates 9r4c5.
The anti-track approach to examining the 59r6c4 pair is to say that by taking the anti-track P'(9r6c4) it is one of the 9s that sees 9r6c4 that you eliminate without yet knowing which one. We then find as a consequence of the development of the anti-track that it is 9r4c5.
Robert

Hi Robert,
You were talking about how to start a whip. You failed to show that it was harder than to start a conjugated tracks. You're now changing the topic. So, what's your point?

And this thread is about Forcing-T&E.

denis_berthier wrote:Hi Robert,
You were talking about how to start a whip. You failed to show that it was harder than to start a conjugated tracks. You're now changing the topic. So, what's your point?

My last comment was a response to your comment that I forgot to quote (I corrected) and not the creation of another topic.
Robert

Mauriès Robert wrote:

denis_berthier wrote:Hi Robert,
You were talking about how to start a whip. You failed to show that it was harder than to start a conjugated tracks. You're now changing the topic. So, what's your point?

My last comment was a response to your comment that I forgot to quote (I corrected) and not the creation of another topic.

Sorry, but I still can't see how your new remarks are in any way related to how to start a whip and how this is different from starting a conjugate pair of tracks

denis_berthier wrote:Sorry, but I still can't see how your new remarks are in any way related to how to start a whip and how this is different from starting a conjugate pair of tracks

Reflection made, you are right there is no difference in the way to start a whip or an antitrack which have vocation to eliminate a target since in one case as in the other the target is necessarily a candidate who sees the candidate of left of V1.
Concerning the subject forcing-T&E I have nothing to add for the moment.
Cordialy
Robert

Mauriès Robert wrote:

denis_berthier wrote:Sorry, but I still can't see how your new remarks are in any way related to how to start a whip and how this is different from starting a conjugate pair of tracks

Reflection made, you are right there is no difference in the way to start a whip or an antitrack which have vocation to eliminate a target since in one case as in the other the target is necessarily a candidate who sees the candidate of left of V1.
Concerning the subject forcing-T&E I have nothing to add for the moment.

Considering that an anti-track is nothing more than a braid with no notion of length and with the loss of a lot of the information found during construction, I don't see how their starting points could be different.
But the discussion was not between whips and antitracks; it was between a whip and a pair of conjugated tracks. You keep repeating that the latter have an easier to find starting point. I've shown that this claim is false.

denis_berthier wrote:But the discussion was not between whips and antitracks; it was between a whip and a pair of conjugated tracks. You keep repeating that the latter have an easier to find starting point. I've shown that this claim is false.

I didn't say anything like that, read what I wrote again.
Robert