X-Cycles questions
Re: X-Cycles questions
re formulated below.
Last edited by StrmCkr on Thu Jan 01, 1970 12:00 am, edited 1 time in total.
Some do, some teach, the rest look it up.
-

StrmCkr - Posts: 1450
- Joined: Tue Sep 05, 2006 4:00 pm
Re: X-Cycles questions
Mino21 wrote:... and please don't tell me that it works also like a weak link ... the whole question of "strong links working as weak links" is totally absent in my logical setting.
Mino, please stop bothering people here, but start to read and understand.
You implemented x-cycles following SudoWiki:
X-Cycles (Part 1): A "Cycle", as the name implies, is a loop or joined-up chain of single digits with alternating strong and weak links.
X-Cycles (Part 2): A discontinuity occurs when we find two strong links next to each other (that is, with no weak link between them) or two weak links next to each other (with no strong link dividing them). These rules work only if there is exactly one discontinuity, and such a loop will always have an odd number of nodes.
Your chain only works, because the strong link in column 2 IS a weak link.
- eleven
- Posts: 3246
- Joined: Sun Feb 10, 2008 5:00 pm
Re: X-Cycles questions
@StrmCkr
it is probably due to the fact that english is not my native language, but honestly I find particularly difficult to fully understand your posts...
which configuration are you referring to exactly?
At this point, however, it cannot be just a question of language barrier, but it is either superficiality or bad faith:
I would answer if I had understood the question...
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
It may seem strange to you, but I used the SudokuWiki site only to understand the basic idea of the various solving techniques, but then, both for x-cycles and some other techniques, I built my own logic settings and algorithms.
Anyway I don't want to bother anyone, if you or someone else doesn't want to answer or thinks I don't deserve an answer, just don't do it...
it is probably due to the fact that english is not my native language, but honestly I find particularly difficult to fully understand your posts...
StrmCkr wrote:Your code shouldn't even be able to build it
which configuration are you referring to exactly?
StrmCkr wrote:(you said you found invalid loops)
At this point, however, it cannot be just a question of language barrier, but it is either superficiality or bad faith:
Mino21 wrote:Maybe I was unclear, maybe also because of my bad english, but the algorithm I implemented does not find either of the two aforementioned loops, as more than two consecutive weak links are not allowed; in fact once arrived at one of these points:
r1c123 = r1c8-r8c8-r8c2 ...
r123c2 = r8c2-r8c8-r1c8 ...
the search for the next node necessarily requires a strong link (in the description of my algorithm it is clearly explained).
StrmCkr wrote:Now your asking to counter prove your software that skips elimination sequences that don't match a preset condition?
I would answer if I had understood the question...
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
eleven wrote:Mino21 wrote:... and please don't tell me that it works also like a weak link ... the whole question of "strong links working as weak links" is totally absent in my logical setting.
Mino, please stop bothering people here, but start to read and understand.
You implemented x-cycles following SudoWiki:
X-Cycles (Part 1): A "Cycle", as the name implies, is a loop or joined-up chain of single digits with alternating strong and weak links.
X-Cycles (Part 2): A discontinuity occurs when we find two strong links next to each other (that is, with no weak link between them) or two weak links next to each other (with no strong link dividing them). These rules work only if there is exactly one discontinuity, and such a loop will always have an odd number of nodes.
Your chain only works, because the strong link IS a weak link.
It may seem strange to you, but I used the SudokuWiki site only to understand the basic idea of the various solving techniques, but then, both for x-cycles and some other techniques, I built my own logic settings and algorithms.
Anyway I don't want to bother anyone, if you or someone else doesn't want to answer or thinks I don't deserve an answer, just don't do it...
- Mino21
- Posts: 35
- Joined: Fri Jul 08, 2022 3:03 pm
Re: X-Cycles questions
hi Mino21, my reading of the diagram:
if r123c2 is not x then r2c8 is x then r9c13 is not x then one of r9c79 is x: it is not known which one
if r123c2 is not x then one of r1c13 is x then r1c7 is not x then one of r2c7 r3c9 is x it is not known which one
in either case the loop can't be built
if r123c2 is not x then r2c8 is x then r9c13 is not x then one of r9c79 is x: it is not known which one
if r123c2 is not x then one of r1c13 is x then r1c7 is not x then one of r2c7 r3c9 is x it is not known which one
in either case the loop can't be built
- P.O.
- Posts: 1951
- Joined: Mon Jun 07, 2021 2:57 am
Re: X-Cycles questions
http://forum.enjoysudoku.com/collection-of-solving-techniques-t3315.html i do suggest looking through this post for everything marked
nice loops, X-cycles for grouped and non grouped and eventually AIC's for reference material that was used by Andrew steward for his wiki page that you are quoting back to us as your source.
I struggle immensely with anything written: I'll attempt to be clear and to the point.
all of use are saying the same thing on the above formation you provided to us.
a box { what i call an empty rectangle intersection ERI}
has 2 truths that can be effectively used
Row is true or the Col is True
forming the strong link
because this box is a strong link the next links must be weak {never a strong link} as they must alternate
strong -> weak , weak -> strong
the only way to link to this box is via Weak links in and out off the Row and Col
my question is why is the diagrams missing the middle cell R1C2
should be listed as (R1C123 = R123C2) as the strong links
vs your version of
R1C123 = R23C2
or
R1C13 = R123C2
the reason i pointed this out is from the 2 string kite diagram that works and the version that will not work as the ERI box can overlap a 2-string kite formation and generate errors if you are not careful to include the centre cell in both directions.
That was my proof of concept that shows a potential flaw in your diagrams then you said you could generate some chains but your code filtered them out as invalid and produced no eliminations based on your linking rules { in-which your linking rules appear muddled};
hence my conundrum of: how do I prove a potential error when you filter errors out already without seeing your code in action to understand what it is doing so I'll digress.
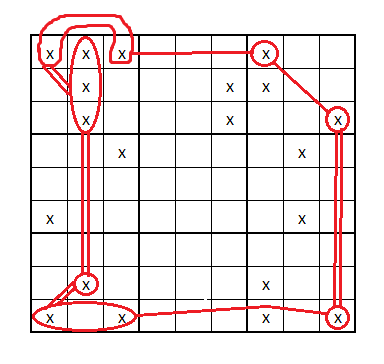
works: however its because the link from Box 1 to box 7 isn't a strong link its actually a weak link {it should be painted a single line not a 2 lines see above note on linking}
I'll modify your image to show case it clearly. -- side note: my codes full eliminations are listed
/ = empty of x
. = potentially has an x
-x is an elimination.
(r1c123 = R123C2 ) - ( R789C2 = R9C123 ) - (R9C9 = R3C9) =>> R1C78,R3C2 <> X
if i add the strong link between the boxes it has no effect.
/ = empty of x
. = potentially has an x
-x is an elimination.
(r1c123 = R123C2 ) - ( R789C2 = R9C123 ) - (R9C9 = R3C9) =>> R1C78,R3C2 <> X
for fun these should work for you as well.
/ = empty of x
. = potentially has an x
-x is an elimination.
1 = 1
. = empty.
-1 = elimination.
nice loops, X-cycles for grouped and non grouped and eventually AIC's for reference material that was used by Andrew steward for his wiki page that you are quoting back to us as your source.

I struggle immensely with anything written: I'll attempt to be clear and to the point.
all of use are saying the same thing on the above formation you provided to us.
a box { what i call an empty rectangle intersection ERI}
has 2 truths that can be effectively used
Row is true or the Col is True
forming the strong link
because this box is a strong link the next links must be weak {never a strong link} as they must alternate
strong -> weak , weak -> strong
the only way to link to this box is via Weak links in and out off the Row and Col
my question is why is the diagrams missing the middle cell R1C2
- Code: Select all
| x x x |
|/ x / |
|/ x / |
should be listed as (R1C123 = R123C2) as the strong links
vs your version of
R1C123 = R23C2
or
R1C13 = R123C2
the reason i pointed this out is from the 2 string kite diagram that works and the version that will not work as the ERI box can overlap a 2-string kite formation and generate errors if you are not careful to include the centre cell in both directions.
That was my proof of concept that shows a potential flaw in your diagrams then you said you could generate some chains but your code filtered them out as invalid and produced no eliminations based on your linking rules { in-which your linking rules appear muddled};
hence my conundrum of: how do I prove a potential error when you filter errors out already without seeing your code in action to understand what it is doing so I'll digress.

works: however its because the link from Box 1 to box 7 isn't a strong link its actually a weak link {it should be painted a single line not a 2 lines see above note on linking}
I'll modify your image to show case it clearly. -- side note: my codes full eliminations are listed
- Code: Select all
------------------------------
| X X X | . . . |-X -X / |
| / X / | . . . | . . / |
| / -X / | . . . | . . x |
------------------------------
| . . . | . . . | . . / |
| . . . | . . . | . . / |
| . . . | . . . | . . / |
------------------------------
| / x / | . . . | . . / |
| / X / | . . . | . . / |
| x x x | . . . | . . x |
------------------------------
/ = empty of x
. = potentially has an x
-x is an elimination.
(r1c123 = R123C2 ) - ( R789C2 = R9C123 ) - (R9C9 = R3C9) =>> R1C78,R3C2 <> X
if i add the strong link between the boxes it has no effect.
- Code: Select all
------------------------------
| X X X | . . . |-X -X / |
| / X / | . . . | . . / |
| / -X / | . . . | . . x |
------------------------------
| . / . | . . . | . . / |
| . / . | . . . | . . / |
| . / . | . . . | . . / |
------------------------------
| / x / | . . . | . . / |
| / X / | . . . | . . / |
| x x x | . . . | . . x |
------------------------------
/ = empty of x
. = potentially has an x
-x is an elimination.
(r1c123 = R123C2 ) - ( R789C2 = R9C123 ) - (R9C9 = R3C9) =>> R1C78,R3C2 <> X
for fun these should work for you as well.
- Code: Select all
------------------------------
| X X X | . . . | . -x . |
| / X / | . . . | . . . |
| / X / | . . . | . . . |
------------------------------
| . . . | . . . | . . . |
| . . . | . . . | . . . |
| . . . | . . . | . . . |
------------------------------
| / x / | . . . | / x / |
| X X X | . . . | x x x |
| / x / | . . . | / x / |
------------------------------
/ = empty of x
. = potentially has an x
-x is an elimination.
- Code: Select all
+----------------+------------+----------------+
| (1) (-1) (1) | -1 -1 -1 | (1) (-1) (1) |
| . (1) . | . . . | . (1) . |
| . (1) . | . . . | . (1) . |
+----------------+------------+----------------+
| . -1 . | . . . | . -1 . |
| . -1 . | . . . | . -1 . |
| . -1 . | . . . | . -1 . |
+----------------+------------+----------------+
| . (1) . | . . . | . (1) . |
| (1) (-1) (1) | -1 -1 -1 | (1) (-1) (1) |
| . (1) . | . . . | . (1) . |
+----------------+------------+----------------+
1 = 1
. = empty.
-1 = elimination.
- Code: Select all
+---------------+---------+---------------+
| -1 (1) -1 | . . . | -1 (1) -1 |
| (1) . (1) | . . . | (1) . (1) |
| -1 (1) -1 | . . . | -1 (1) -1 |
+---------------+---------+---------------+
| . . . | . . . | . . . |
| . . . | . . . | . . . |
| . . . | . . . | . . . |
+---------------+---------+---------------+
| -1 (1) -1 | . . . | -1 (1) -1 |
| (1) . (1) | . . . | (1) . (1) |
| -1 (1) -1 | . . . | -1 (1) -1 |
+---------------+---------+---------------+
Some do, some teach, the rest look it up.
-

StrmCkr - Posts: 1450
- Joined: Tue Sep 05, 2006 4:00 pm
Re: X-Cycles questions
This is not a cycle because box 3 does not connect to box 1.
It would be better to name it forcing x-chain.
You could start reasoning at the -X. a(net gives contradiction) -> -a
If you want to display multiple eliminations, you can do a(direct) intersect -a(net) -> -x, but then you need to take care of contradictions in your net/chain.
The cycle part is just a rare case where eliminations fall outside the chain. Cycle check is slower and harder to implement than a forcing net.
1. One way to implement real cycles is build forcings (true->false or false->true).
2. Then combine into a node that allows both directions (node = case 1 + case 2).
3a. A bad way is then to recursive find a next linking node till you are at your start node.
3b. A better way is to build a net (bit like single coloring) which prevents slow recursive loops. But finding the loops when the net finds a contradiction (one color must be false) is much harder. (Then fallback to recursive loops?)
Finding first a contradiction does not mean the loop cannot form.
So do you want to find all loops or just like SudokuWiki only the first thing it find which is most of the time a contradiction (rule 1, 2)?
Rule 1 and 2 can use the same net but you can find more exclusions building an one-direction forcing net.
This is still all easy compared to when you want truth/link logic, which If don't know how to implement fully/fast.
How did you (StrmCkr) solve the problem of those early contradictions which prevents forming nice loops?
Is your solver public somewhere (Mino21)?
- Code: Select all
------------------------------
| X X X | . . . |-X -X / |
| / X / | . . . | . . / |
| / -X / | . . . | . . x |
------------------------------
| . . . | . . . | . . / |
| . . . | . . . | . . / |
| . . . | . . . | . . / |
------------------------------
| / x / | . . . | . . / |
| / X / | . . . | . . / |
| x x x | . . . | . . x |
------------------------------
It would be better to name it forcing x-chain.
You could start reasoning at the -X. a(net gives contradiction) -> -a
If you want to display multiple eliminations, you can do a(direct) intersect -a(net) -> -x, but then you need to take care of contradictions in your net/chain.
The cycle part is just a rare case where eliminations fall outside the chain. Cycle check is slower and harder to implement than a forcing net.
1. One way to implement real cycles is build forcings (true->false or false->true).
2. Then combine into a node that allows both directions (node = case 1 + case 2).
3a. A bad way is then to recursive find a next linking node till you are at your start node.
3b. A better way is to build a net (bit like single coloring) which prevents slow recursive loops. But finding the loops when the net finds a contradiction (one color must be false) is much harder. (Then fallback to recursive loops?)
Finding first a contradiction does not mean the loop cannot form.
So do you want to find all loops or just like SudokuWiki only the first thing it find which is most of the time a contradiction (rule 1, 2)?
Rule 1 and 2 can use the same net but you can find more exclusions building an one-direction forcing net.
This is still all easy compared to when you want truth/link logic, which If don't know how to implement fully/fast.
How did you (StrmCkr) solve the problem of those early contradictions which prevents forming nice loops?
Is your solver public somewhere (Mino21)?
- creint
- Posts: 400
- Joined: Sat Jan 20, 2018 2:28 pm
Re: X-Cycles questions
This is not a cycle because box 3 does not connect to box 1.
my interpretation is that it does by the weak link of r1c78 seeing strong links of box 1 and col 9.
R1c78 - (r1c123 = R123C2 ) - ( R789C2 = R9C123 ) - (R9C9 = R3C9) - R1C78 =>> R1C78,R3C2 <> X
the red cell would need another chain to prove it reading this left to right or right to left is r1c78 as true implies r1c78 is also false.
which acts more like a forcing network which is how I've viewed the notation of nice/loops and x-cycles to be written as the elimination proves its self false as its usually listed twice at start and end closing a loop
- Code: Select all
------------------------------
| X X X | . . . |-X -X / |
| / X / | . . . | . . / |
| / -X / | . . . | . . x |
------------------------------
| . . . | . . . | . . / |
| . . . | . . . | . . / |
| . . . | . . . | . . / |
------------------------------
| / x / | . . . | . . / |
| / X / | . . . | . . / |
| x x x | . . . | . . x |
------------------------------
mines built around Aic logic starting only off strong links recognizing cannibalistic and internal eliminations from sub-chains.
eri -> eri -> strong link on col =>> eliminating common points from starting cells in box 1 and end point r3c9 => R1C78
my eliminations walk the links backwards once built and removes internal eliminations as well. start of r3c9 -> end point of box 8{col} removes peers
a nice loop/x-cycle approach should need 2-3 chains to do this depending if it can group weak links r1c78 together or not.
care to elaborate?How did you (StrmCkr) solve the problem of those early contradictions which prevents forming nice loops?
how mine works: Show
Some do, some teach, the rest look it up.
-

StrmCkr - Posts: 1450
- Joined: Tue Sep 05, 2006 4:00 pm
Re: X-Cycles questions
@StrmCkr
first of all I want to say that I really appreciate your effort to help me.
Me too I will try to be as clear as possible in this post.
As already mentioned, I want to point out that my goal is not solving sudokus in general, I just enjoy implementing logic problems in C/C++, and sudoku is one of them.
Before looking on the internet I had already implemented the basic strategies, which I later learned are called: Naked Candidates, Hidden Candidates, Intersection Removal, Avoidable Rectangles, Unique Rectangles (basic cases), plus my own version of a brute force algorithm used when all resolution techniques fail.
At that point I started looking for advanced solving techniques and stumbled upon the SudokuWiki site, which I found well done.
As already mentioned, however, I have often used it only to understand the basic idea of the various resolution techniques (in some cases I have only looked at the images, also considering my difficulties with english), to then build my own personal logic approach and algorithm. This is also what happened with the x-cycles, in fact the concepts of "alternating strong_link-weak_link", "discontinuity" and "strong links acting as weak links" are completely absent in my approach and were not necessary for my problem modeling, which I report for convenience:
Let me clarify some points that may not be very clear:
- the demonstration of the loop rules (having used SudokuWiki as a source, by convention I used as names those reported in the aforementioned site) in point c) are a consequence of the positions contained in points a) and b).
In particular:
- when a mini-row and a mini-column have a cell in common as in this case:
I cannot consider the strong link r1c123=r123c2 cause if r1c2 is solution then the logic inference A=>!B, reported at point a), is not respected. This is the reason why I split r1c123=r123c2 in r1c123=r23c2 and r1c13=r123c2.
And with this I believe and hope to have clarified everything that needed to be clarified.
Now let's move on to the various candidates configurations you posted:
About the last two examples with 1 you posted I did not understand what they represent.
So in the end my approach seems to work with all the examples you posted, am I wrong?
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Hi P.O., if you're referring to this, we can built the following loop:
r123c2=r8c2=r9c13-r9c9=r3c9-r1c7-r1c13=r123c2
So we have a loop rule 3 with elimination in r1c7.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
No, I still have to fix various things.
Anyway, given that I have not yet studied AICs and other advanced strategies, in this message I have explained how I have implemented x-cycles.
first of all I want to say that I really appreciate your effort to help me.
Me too I will try to be as clear as possible in this post.
As already mentioned, I want to point out that my goal is not solving sudokus in general, I just enjoy implementing logic problems in C/C++, and sudoku is one of them.
Before looking on the internet I had already implemented the basic strategies, which I later learned are called: Naked Candidates, Hidden Candidates, Intersection Removal, Avoidable Rectangles, Unique Rectangles (basic cases), plus my own version of a brute force algorithm used when all resolution techniques fail.
At that point I started looking for advanced solving techniques and stumbled upon the SudokuWiki site, which I found well done.
As already mentioned, however, I have often used it only to understand the basic idea of the various resolution techniques (in some cases I have only looked at the images, also considering my difficulties with english), to then build my own personal logic approach and algorithm. This is also what happened with the x-cycles, in fact the concepts of "alternating strong_link-weak_link", "discontinuity" and "strong links acting as weak links" are completely absent in my approach and were not necessary for my problem modeling, which I report for convenience:
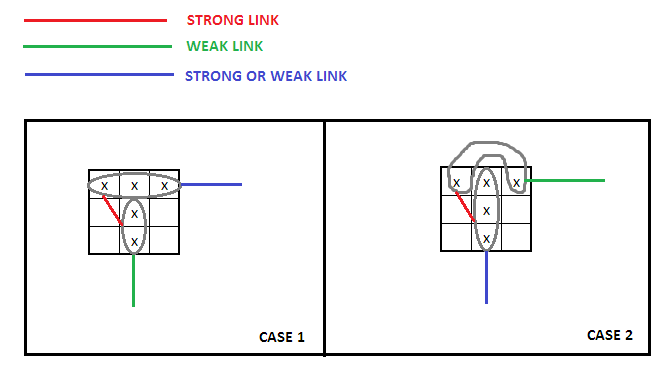
Mino21 wrote:a) only two candidates in an unit imply a strong link and hence the following two logical implications:
- Code: Select all
A => !B
!A => B
more than two candidates in a unit imply a weak link and hence the only following logical implication:
- Code: Select all
A => !B
b) a valid loop must have the following characteristics:
- at least 4 nodes;
- at least a weak link;
- at most an even subsequence of consecutive strong links or a subsequence of two consecutive weak links;
- (any number of odd subsequences of consecutive strong links).
c) loop rules (green=true and red=false; arrows indicate the starting point and the direction of the logical inferences):
d) implemented recursive algorithm about x-cycles (not grouped):
- I always start from a strong link, of which a candidate will be the arrival node that closes the loop, while I pass the other to the recursive function that, node by node, tries to build a loop;
- at each recursive call, I first use the information on the part of the loop constructed so far to deduce (using positions contained in point b)) if the next link can be weak or must necessarily be strong;
- then I derive the type of connection (weak or strong) that I would have in the other units to which the previous node belongs, and check that it is compatible with the result illustrated in the previous point;
- if it is compatible I consider the various candidates in that unit one at a time, and if the candidate considered is not already a node I add it to the cycle;
- at this point if the loop isn't closed I go on with other recursive calls.
with the specification that with grouped-x-cycles in the case of mini rows and mini columns that share a cell, it is necessary to consider the two cases obtained by assigning the common cell once to the horizontal group and once to the vertical one, as shown in the following image:
Let me clarify some points that may not be very clear:
- the demonstration of the loop rules (having used SudokuWiki as a source, by convention I used as names those reported in the aforementioned site) in point c) are a consequence of the positions contained in points a) and b).
In particular:
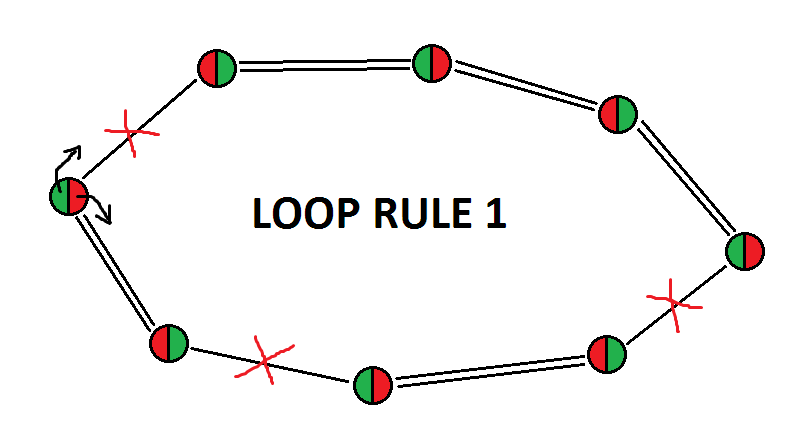
loop rule 1 is characterized by:
1) at least one weak link;
2) no subsequence of two consecutive weak links;
3) no even subsequence of consecutive strong links;
4) any number of odd subsequences of consecutive strong links;
5) even number of nodes (but this is a consequence of the previous points)
Proof: starting from a node belonging to a weak link, assuming once it is true and once it is false, and using the logical inferences contained in point a), we will obtain two perfectly mirror chains, which will allow us to eliminate the candidates in the unit to which the weak links belong (of course I am referring to the cells that are not nodes).
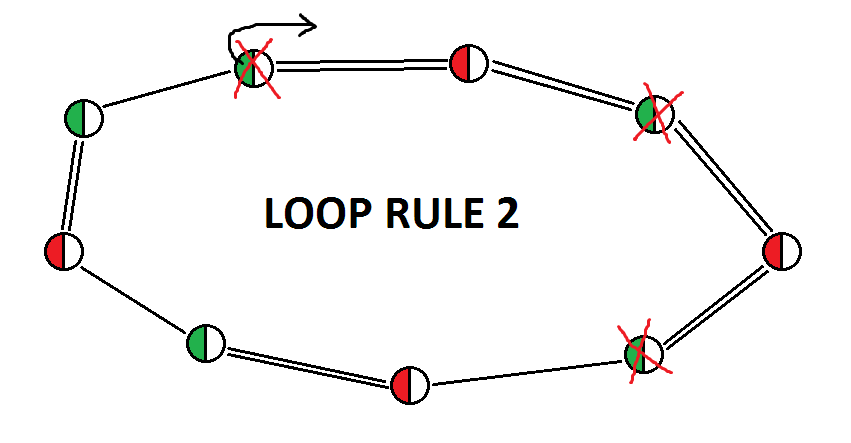
loop rule 2 is characterized by:
1) at least one weak link;
2) no subsequence of two consecutive weak links;
3) one even subsequence of consecutive strong links;
4) any number of odd subsequences of consecutive strong links;
5) odd number of nodes (but this is a consequence of the previous points)
Proof: starting from the node that starts the even subsequence of consecutive strong links, and assuming it is true, we will obtain a contradiction, which will allow us to eliminate the candidates in the nodes marked as true and that belong to the even subsequence of consecutive strong links.
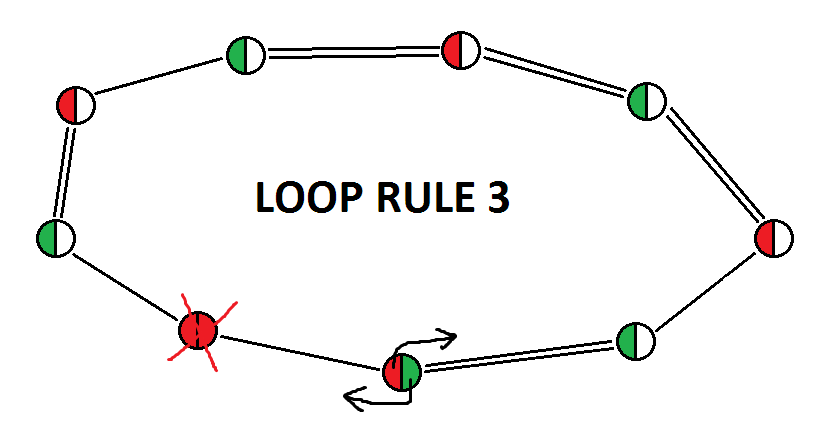
loop rule 3 is characterized by:
1) at least one weak link;
2) one subsequence of two consecutive weak links;
3) no even subsequence of consecutive strong links;
4) any number of odd subsequences of consecutive strong links;
5) odd number of nodes (but this is a consequence of the previous points)
Proof: starting from the node that starts the subsequence of two consecutive weak links, and assuming once it is true and once it is false, we will obtain that the node that sees two weak links is false in both cases, which will allow us to eliminate the candidate in it;
- when a mini-row and a mini-column have a cell in common as in this case:
- Code: Select all
---------
| x x x |
| / x / |
| / x / |
---------
I cannot consider the strong link r1c123=r123c2 cause if r1c2 is solution then the logic inference A=>!B, reported at point a), is not respected. This is the reason why I split r1c123=r123c2 in r1c123=r23c2 and r1c13=r123c2.
And with this I believe and hope to have clarified everything that needed to be clarified.
Now let's move on to the various candidates configurations you posted:
StrmCkr wrote:
- Code: Select all
-------------------------
| X X X | . . . |-X-X / |
| / X / | . . . | . . / |
| /-X / | . . . | . . x |
-------------------------
| . . . | . . . | . . / |
| . . . | . . . | . . / |
| . . . | . . . | . . / |
-------------------------
| / x / | . . . | . . / |
| / X / | . . . | . . / |
| x x x | . . . | . . x |
-------------------------
I try to explain how my algorithm works in this case:
- as mentioned in point d), I always start from a strong link, for example the one in c9, and let r9c9 be the arrival node and r3c9 the starting node;
- from the data on the part of the cycle constructed so far, I deduce that the next link can also be weak (ALSO WEAK) and not necessarily strong (ONLY STRONG);
- considering all the possible connections from r3c9, at a certain point I add the node r1c78 with a weak link (-r1c78);
...going on with the notation introduced in the previous two lines...
- ALSO WEAK;
- -r1c123;
- ONLY STRONG;
- =r23c2;
- ALSO WEAK;
- -r78c2;
- ONLY STRONG;
- =r9c123;
- ALSO WEAK;
- -r9c9;
- the chain is closed, I check loop is valid and I deduce that it is a loop rule 3 that delete candidates in r1c78.
To sum up:
r9c9=r3c9-r1c78-r1c123=r23c2-r78c2=r9c123-r9c9
L.R.3 (loop rule 3): r1c78 (elimination)
The aforementioned cycle does not allow me to delete candidate in r3c2, but this other cycle yes:
r9c9=r3c9-r3c2-r789c2=r9c13-r9c9
L.R.3: r3c2
StrmCkr wrote:
- Code: Select all
-------------------------
| X X X | . . . |-X-X / |
| / X / | . . . | . . / |
| /-X / | . . . | . . x |
-------------------------
| . / . | . . . | . . / |
| . / . | . . . | . . / |
| . / . | . . . | . . / |
-------------------------
| / x / | . . . | . . / |
| / X / | . . . | . . / |
| x x x | . . . | . . x |
-------------------------
r9c9=r3c9-r1c78-r1c123=r23c2-r78c2=r9c123-r9c9
L.R.3: r1c78
r9c9=r3c9-r3c2-r789c2=r9c13-r9c9
L.R.3: r3c2
StrmCkr wrote:
- Code: Select all
-------------------------
| X X X | . . . | .-x . |
| / X / | . . . | . . . |
| / X / | . . . | . . . |
-------------------------
| . . . | . . . | . . . |
| . . . | . . . | . . . |
| . . . | . . . | . . . |
-------------------------
| / x / | . . . | / x / |
| X X X | . . . | x x x |
| / x / | . . . | / x / |
-------------------------
r8c123-r8c789=r79c8-r1c8-r1c123=r23c2-r79c2=r8c123
L.R.3: r1c8
About the last two examples with 1 you posted I did not understand what they represent.
So in the end my approach seems to work with all the examples you posted, am I wrong?
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
P.O. wrote:hi Mino21, my reading of the diagram:
if r123c2 is not x then r2c8 is x then r9c13 is not x then one of r9c79 is x: it is not known which one
if r123c2 is not x then one of r1c13 is x then r1c7 is not x then one of r2c7 r3c9 is x it is not known which one
in either case the loop can't be built
Hi P.O., if you're referring to this, we can built the following loop:
r123c2=r8c2=r9c13-r9c9=r3c9-r1c7-r1c13=r123c2
So we have a loop rule 3 with elimination in r1c7.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
creint wrote:Is your solver public somewhere (Mino21)?
No, I still have to fix various things.
Anyway, given that I have not yet studied AICs and other advanced strategies, in this message I have explained how I have implemented x-cycles.
- Mino21
- Posts: 35
- Joined: Fri Jul 08, 2022 3:03 pm
Mino21 wrote:eleven wrote:Mino21 wrote:at this point:
- Code: Select all
+------------------+-------------------+--------------------+
| 1 8 5 | 49 2 6 | 3 7 49 |
| 234 6 234 | 34579 134 13457 | 2458 28 24589 |
| 234 9 7 | 345 34 8 | 1 26 2456 |
+------------------+-------------------+--------------------+
| 4678 1 48 | 348 5 2 | 68 9 37 |
| 245789 27 2489 | 348 6 34 | 258 13 137 |
| 2568 3 28 | 1 7 9 | 2568 4 2568 |
+------------------+-------------------+--------------------+
| 2378 4 1 | 6 38 37 | 9 5 238 |
| 23789 27 2389 | 3457 1348 13457 | 2468 12368 123468 |
| 38 5 6 | 2 9 134 | 7 138 1348 |
+------------------+-------------------+--------------------+
the program returns the following invalid cycle ("=' strong link, '-' weak link):
- Code: Select all
START: r5c9==r5c8==(r8c8 r9c8)--(r8c8 r8c9)==(r8c5 r8c6)==r9c6==(r9c8 r9c9)--(r8c9 r9c9)==r5c9
more or less I think I understand why it is not a valid loop_rule_1, but I don't know what condition exactly I should add to my algorithm to have only valid loops.
I think the problem is related to the group-nodes that share a same candidate, but I honestly don't know what to do.
"(r8c8 r9c8)--(r8c8 r8c9)"
This is not a weak link.
Weak link would mean, that if a digit is on one side, it cannot be on the other side.
But r8c8 is on both sides.
Okay
and I assume that the same reasoning would have applied even if the link had been strong
wrong.
"strong link" can share cells.
-

Pat - Posts: 4056
- Joined: Mon Jul 18, 2005 4:00 pm
Mino21 wrote:Isn't this:Mino21 wrote:two consecutive group-nodes
cannot have a cell in common
a consequence of this:eleven wrote:"(r8c8 r9c8)--(r8c8 r8c9)"
This is not a weak link, which would mean, that if a digit is on one side, it cannot be on the other side. But r8c8 is on both sides.
?
no, it is not a consequence:
what about a "strong link"?
-

Pat - Posts: 4056
- Joined: Mon Jul 18, 2005 4:00 pm
Re: X-Cycles questions
hi Mino21, you wrote: r123c2=r8c2=r9c13-r9c9=r3c9-r1c7-r1c13=r123c2
i have some difficulty in understanding your notation: what does the sign = mean between r123c2 and r8c2 and what does the same = sign mean between r8c2 and r9c13 ?
i have some difficulty in understanding your notation: what does the sign = mean between r123c2 and r8c2 and what does the same = sign mean between r8c2 and r9c13 ?
- P.O.
- Posts: 1951
- Joined: Mon Jun 07, 2021 2:57 am
Re: X-Cycles questions
StrmCkr wrote:
the way i would read this is
R8C123(on) => r8c789{off} => r79c8 (on) => r1c8 (off). {stalls on the weak link here}
then you added on to the end the other direction the links back to r8c123 that swap it to "on"
R1c123 {off} => r23C2(on) => r79c2(off) => r8c123(on)
if i wasn't attempting to digest your output:
id read that you started on a weak link and not a strong link as its a group of cells linking with the - {not} true indicator vs = (or)
if it started on a strong link it should read
(r79c2 = r8c123) - etc
this grid should only have 2 possible read outs : this and the same chain written backwards right -> left
r1c8 - (r1c123=r123c2) - (r789c2 = r8c123) - (r8c789=r789c8) -r1c8 =>> r1c8 <> x
this is a grouped discontinuous X-cycle/ x-chain / nice loop.
to make yours make more sense to what its doing i believe that 2nd part of your chain actually belongs in the front
{delete the first link as its repeated, paste in the terminated weak spot and the last section you added after it hits a weak link with no more links.)
r1c8 - (r1c123=r23c2) - (r79c2=r8c123) - (r8c789=r79c8) - r1c8
which looks exactly like mine with the exception your not including the "middle" cell(s).
{cross checked yzf's solver and they are also not including the middle cell on both sides}
r1c78-r1c123=r23c2-r78c2=r9c123-r9c9=r3c9-r1c78
looks familiar
suspecting you might have an output translation error with the way your code operates.
- Code: Select all
-------------------------
| X X X | . . . | .-x . |
| / X / | . . . | . . . |
| / X / | . . . | . . . |
-------------------------
| . . . | . . . | . . . |
| . . . | . . . | . . . |
| . . . | . . . | . . . |
-------------------------
| / x / | . . . | / x / |
| X X X | . . . | x x x |
| / x / | . . . | / x / |
-------------------------
r8c123-(r8c789=r79c8)-r1c8-(r1c123=r23c2)-(r79c2=r8c123)
L.R.3: r1c8
the way i would read this is
R8C123(on) => r8c789{off} => r79c8 (on) => r1c8 (off). {stalls on the weak link here}
then you added on to the end the other direction the links back to r8c123 that swap it to "on"
R1c123 {off} => r23C2(on) => r79c2(off) => r8c123(on)
if i wasn't attempting to digest your output:
id read that you started on a weak link and not a strong link as its a group of cells linking with the - {not} true indicator vs = (or)
if it started on a strong link it should read
(r79c2 = r8c123) - etc
this grid should only have 2 possible read outs : this and the same chain written backwards right -> left
r1c8 - (r1c123=r123c2) - (r789c2 = r8c123) - (r8c789=r789c8) -r1c8 =>> r1c8 <> x
this is a grouped discontinuous X-cycle/ x-chain / nice loop.
to make yours make more sense to what its doing i believe that 2nd part of your chain actually belongs in the front
{delete the first link as its repeated, paste in the terminated weak spot and the last section you added after it hits a weak link with no more links.)
r1c8 - (r1c123=r23c2) - (r79c2=r8c123) - (r8c789=r79c8) - r1c8
which looks exactly like mine with the exception your not including the "middle" cell(s).
{cross checked yzf's solver and they are also not including the middle cell on both sides}
- Grouped Discontinuous Nice Loop: r1c8<>1
1r1c8 - r789c8 = r8c79 - r8c123 = r79c2 - r123c2 = r1c13 - 1r1c8
Grouped Discontinuous Nice Loop: r1c8<>1
1r1c8 - r1c123 = r23c2 - r789c2 = r8c13 - r8c789 = r79c8 - 1r1c8
To sum up:
r9c9=r3c9-r1c78-r1c123=r23c2-r78c2=r9c123-r9c9
L.R.3 (loop rule 3): r1c78 (elimination)
r1c78-r1c123=r23c2-r78c2=r9c123-r9c9=r3c9-r1c78
looks familiar
suspecting you might have an output translation error with the way your code operates.
Some do, some teach, the rest look it up.
-

StrmCkr - Posts: 1450
- Joined: Tue Sep 05, 2006 4:00 pm
Re: X-Cycles questions
Mino21 wrote:It may seem strange to you, but I used the SudokuWiki site only to understand the basic idea of the various solving techniques, but then, both for x-cycles and some other techniques, I built my own logic settings and algorithms.
lol, you didn't even understand the most basic logic definition of a strong link, ignored all the posts addressing it and insisted on your own weird one. This is the cause of all your troubles.
- eleven
- Posts: 3246
- Joined: Sun Feb 10, 2008 5:00 pm
- i don't know the SudokuWiki definitions;
what i gave above (Grouped x-cycle)
points to Forcing chains: Terminology and Definition
-

Pat - Posts: 4056
- Joined: Mon Jul 18, 2005 4:00 pm
Return to Help with puzzles and solving techniques
Who is online
Users browsing this forum: No registered users and 0 guests